cryptography

中文里「密码」其实是个有点复杂的词，包含了好几种意思，而且这些意思可能看似差不多，但实质上却完全不同，因此在中文社区的讨论里经常会出现各种误会或者错用。例如登录某些软件时需要输入的用户名和密码，刷卡或者 ATM 取钱输入的密码，他们的本质实际上是「口令」，对应英文中的「password」，「passcode」，「pin」等。又比如 DNA 遗传密码，它其实是将蛋白质的构成信息转换为碱基序列并记录下来，本质是一种「编码」，对应英文中的 「encoding」。而这篇文章主要讲的「密码技术」，或者说「加密技术」，对应英文中的「cryptography」，它是为了让信息在传输中能够保证其机密性（confidentiality）而诞生的。

在介绍密码技术之前，有几个基本概念要先理清楚。

Table of Contents

凯撒密码 Caesar cipher

凯撒密码是一种非常简单易懂的加密方式，据说凯撒曾使用过，它的实现方式很简单，就是将明文中的字母表按照一定的字数平移来进行加密的，例如将字母表平移三位，那么 A 就对应了 D，B 对应 E...以此类推。

而解密的过程就是进行反向的操作，在这个场景里，「将各个字母按照字母表进行平移」这个不变的思路，就是密码算法，双方必须事先约定好「平移的位数为 3」，不同的双方可能会有不同的约定，这本质上就是「密钥」。

简单替换密码

按照一个双方约定好的替换表来对每一个字母进行替换，例如 A-Z 双方约定好将顺序倒过来对应着 Z-A，当明文为 A 时，通过替换生成了密文 Z，在收到密文后再进行替换就获得了明文 A。

这个场景里，「按照替换表对字母进行替换」就是密码算法，而具体的「替换表」就是密钥。

通过将密码算法和密钥进行分开考虑，使得一个密码算法可以被重复使用，并且通过可变的密钥来减少重复使用的风险，否则每次加密都要使用一个新的密码算法，那就太麻烦了。

对称密码（用相同的密钥进行加密和解密）

密码技术是为了保证信息传输的安全，因此必须要有将密文恢复成明文的解密能力，而不能单纯的打乱，使用相同的密钥来进行加密和解密的方式，就叫对称密码。

在计算机世界里，计算机所操作的对象，从文本变成了二进制的比特序列，而将文本、图像、音乐等现实中的东西映射为比特序列的操作，就叫编码（encoding）。

而对比特序列进行加密，就必须要提到异或（XOR）运算。XOR 运算的规则非常简单

0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0

可以将其理解为类似黑白棋的翻转，翻转 0 次和 2 次的结果一定是和初始状态一样的。而对比特序列的 XOR 运算就是对每一个相应的比特进行 XOR 运算，和加法不同，XOR 运算中不存在进位。由于两个相同的数进行 XOR 运算的结果一定为 0，因此如果将 A 和 B 的 XOR 运算结果再同 B 进行一次 XOR 运算那么结果就会变回 A，也就是说 A XOR B XOR B 中的两个 B 互相抵消了。

可以看到这上面的步骤和加密解密的步骤非常相似：

一次性密码本

可以看到如果密钥是一个完全随机的二进制比特序列，仅仅使用异或运算就可以实现一个高强度的密码，一次性密码本就是运用这种思路实现的。即使运算能力无穷大的计算机，可以瞬间遍历所有的密钥空间，也依然无法判断所有的结果中哪一个才是正确的明文，因此一次性密码本是无条件安全（unconditionally secure），在理论上无法破译的（theoretically unbreakable），并由香农在 1949 年通过数学方法证明。

但在现实中，这种方式基本没有被使用，因为存在密钥的配送问题。试想如果有一种绝对安全的方式来传输密钥，保证其不被第三方获取，那么为什么不直接用这种方式来传输明文呢？而且密钥和明文的长度相等，密钥保护着明文的机密性，因此也必须妥善保存，如果有办法安全保存和明文一样长的密钥，那不就也有方法来保存明文本身了吗？另外还存在密钥的重用、同步和生成等问题，因此在现实中这种加密方式是基本没有使用场景的。

其他对称加密算法

除了一次性密码本以外，还有 DES（Data Encryption Standard），三重 DES，AES（Advanced Encryption Standard）等其他对称加密算法，这几个基本都是针对固定长度的数据进行加密，当需要加密的明文超过了这个长度时，就需要进行分组。

分组密码和流密码

分组密码（block cipher）是每次只处理特定长度的一块数据数据的一类密码算法，这里的一块数据，就是一个分组，一个分组的比特数，就是分组长度（block length），像 DES，AES 都是这种方式。

流密码（stream cipher）是对数据流进行连续处理的一类密码算法，一般以 1 比特、8 比特或 32 比特为单位进行加密解密，它需要一个内部的状态来记录进度。像一次性密码本就属于流密码。

非对称密码

使用对称密码，就一定会碰到密钥配送问题（key distribution problem），即使用对称密码加密，在解密时就必须要获得加密时相同的密钥，也就是说密文需要和密钥一同传输，才能完成解密，但如果同时传输，一旦被第三方获取，他们也可能通过密钥来完成解密。虽然第三方也许无法推测使用了什么密码算法，但是密码算法本身应该是以公开为前提的，而不应该采用隐蔽式安全性（security by obscurity）来保证。密钥必须被发送，但又不能发送，这就是密钥配送问题。

使用公钥密码（public key cryptography）可以解决密钥配送问题。我们把密钥分为加密密钥和解密密钥两种，发送者使用加密密钥加密，接收者使用解密密钥来解密，可以发现：

也就是说解密密钥一开始就是由接收者自己保管的，只需要将加密密钥交给发送者就可以解决密钥配送问题了。加密密钥和解密密钥是一一对应的，也被成为公钥和私钥（private key），这一对统称为密钥对（key pair），因为数学上的关系，他们也是不能分别单独生成的。

非对称密码还有各种不同的称谓，例如公钥密码。私钥这个术语也有很多别名，例如个人密钥、私有密钥、非公开密钥等，也有人将其称为秘密密钥（secret key），私钥依然还是使用最广泛的，也是最不容易引起歧义的名称。

公钥密码解决了密钥配送问题，但由于需要判断所得到的公钥是否是正确合法的，这个问题被称为公钥认证问题。另外还有一个小问题是非对称加密的处理速度只有对称加密的几百分之一。

RSA

RSA 是目前使用最广泛的公钥密码算法，它的名字取自三位开发者 Ron Rivest，Adi Shamir 和 Leonard Adleman，即 Rivest-Shamir-Adleman 算法。

在 RSA 中，明文、密文和密钥都是数字，它的加密过程涉及到取余运算，可以用下面这个公式来表示：

密文 = 明文^E mod N

也就是说 RSA 的密文是对代表明文的数字的 E 次方求 mod N 的结果，也就是将明文和自己做 E 次乘法，然后将结果除以 N 求余数，这个余数就是密文，就这么简单。

只要知道了 E 和 N 两个数，任何人都可以完成加密运算，所以 E 和 N 就是 RSA 加密的密钥，即 E 和 N 的组合就是公钥。顺便一说，E 就是 Encryption 的首字母，N 是 Number 的首字母。

而 RSA 的解密也非常简单：

明文 = 密文^D mod N

对表示密文的数字的 D 次方求 mod N 就可以得到明文。这里的 N 和加密时的 N 是相同的。D 和 N 的组合就是解密密钥，即私钥，D 也是 Decryption 的首字母。

由于 (E, N) 和 (D, N) 就是公钥和私钥，这三个数字并不是任意的数字都可以，求这三个数字的过程就是生成密钥对的过程。

具体的数学过程和证明这里略去，有兴趣可以自行搜索。

除了 RSA 算法以外，还有很多其他的公钥密码算法，例如 ElGamal 算法，RSA 是利用了质因数分解的困难度，而它利用了 mod N 下求离散对数的困难度，像 GPG 就支持这种方式，它有个缺点是经过加密的密文长度会变为明文的两倍。

还有 Rabin 算法，利用了 mod N 下求平方根的困难度。破译它的困难度和质因数分解是相当的。

椭圆曲线密码，通过将椭圆曲线上的特定点进行特殊的乘法运算来实现的，它的特点是所需的密钥长度比 RSA 短。

中间人攻击 Man-In-The-Middle attack

在数学上针对 RSA 的高效破解算法目前是不存在的，但存在一种中间人攻击。即主动攻击者混入发送者和接收者的中间，对发送者伪装成接收者，对接收者伪装成发送者。中间人把自己的公钥发送给双方后，后续就可以拦截并伪造一份信息再用公钥加密发送给接收者，使得接收者收到了虚假的信息。

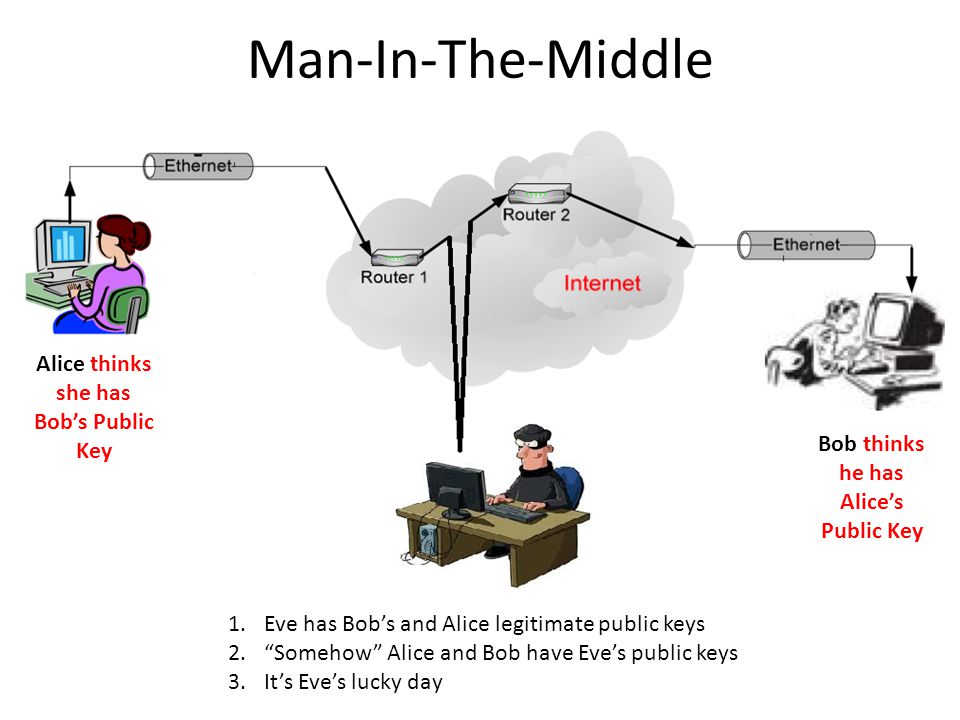
这种攻击不仅针对 RSA，可以针对任何公钥密码，这个过程中公钥密码并没有被破解，所有的加密算法也都正常工作并确保了机密性，但无法保证接收者的信息一定来自发送者。仅靠公钥密码，是无法防御中间人攻击的。要解决这个问题，就需要一种手段来确认公钥是否来自正确的人，这种手段就是认证。

混合加密

通过公钥密码可以解决密钥配送问题，但还有两个很大的问题：

针对计算速度的问题，可以使用混合加密系统。结合对称密码和非对称密码的优势。它主要的流程是：

  1. 通过伪随机生成器来生成一个临时的会话密钥（session key）
  2. 使用会话密钥来对称加密消息
  3. 使用公钥来加密会话密钥
  4. 同时发送 2 和 3 组合的密文

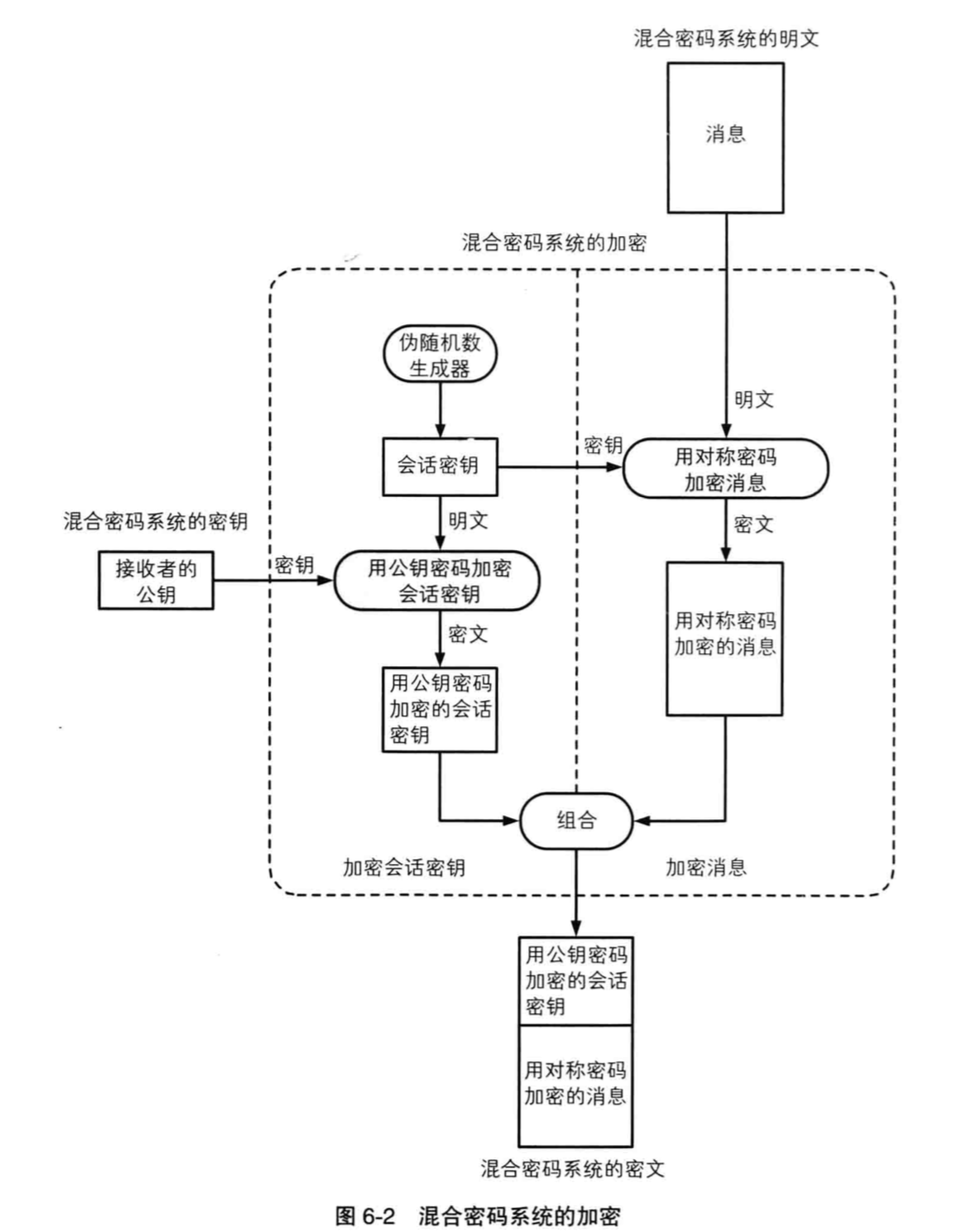
理解了加密之后，解密也就不难理解了。由于公钥密码只用来加解密临时的会话密钥，而会话密钥的长度一般相比与消息的正文是短的多的，因此计算消耗的时间就可以接受了。

著名的 PGP 加密软件，互联网的信息安全基石 SSL/TLS 都使用了混合加密系统。

关于认证

要确保数据没有被篡改，这种性质被称为完整性（integrity），也称为一致性。保证完整性的同时，也需要考虑到效率问题，如果一个文件非常巨大，需要有一种快速的方式来确认，就好像我们要确认是不是同一个人可以通过指纹一样，要是文件也有指纹，就非常方便了。

单向散列函数

单向散列函数（one-way hash function）就是这样一种采集文件指纹的技术。它接受消息（message）作为输入，输出的散列值（hash value）就相当于指纹了。同时散列值的长度和输入的消息长度无关，总是一个固定的长度。

单向散列函数也被称为消息摘要函数（message digest function），哈希函数或者杂凑函数。

输入的消息，也称为原像（pre-image）。

而输出的散列值，也称为消息摘要（message digest）或者指纹（fingerprint）。

单向散列函数有非常多的实现

单向散列函数可以辨别出「篡改」，但还是无法辨别「伪装」，因此仅靠完整性检测是不够的，我们还需要进行认证。用于认证的技术包括消息验证码和数字签名。

消息认证码

消息的认证（authentication），指的是「消息来自正确的发送者」这一性质。

消息认证码（message authentication code）是一种确认完整性并进行认证的技术，简称为 MAC。

消息认证码的输入包括「任意长度的消息」和「一个发送者与接收者之间共享的密钥」，它可以输出任意长度的数据，这个数据被称为 MAC 值。

消息认证码的使用，需要双方共享密钥，然后发送者将计算出的 MAC 值同消息一起发送给接收者，接收者再通过共享密钥根据消息重新计算 MAC 值，比较这两个 MAC 值就知道消息有没有被篡改。

可以看到，既然需要共享密钥，那么必然也存在密钥配送问题，因此也需要使用公钥密码之类的安全方式来发送密钥。

消息认证码的应用实例：

消息认证码可以使用 SHA-1，MD5 之类的单向散列函数实现，其中一种叫做 HMAC，也可以使用 DES，AES 之类的分组密码，当然也可以使用流密码或公钥密码等方式。

针对消息认证码的攻击，可以使用重放攻击（replay attack）和密钥推测攻击。

当然，消息认证码也存在无法解决的问题，比如「对第三方证明」和「防止否认」（nonrepudiation）。这就需要使用数字签名来解决了。

数字签名

数字签名相当于现实中的盖章、签字，它不仅可以识别篡改和伪装，还可以防止否认。消息认证码之所以无法防止否认，是因为共享密钥的存在，接收者和发送者都可以计算出正确的 MAC 值，而对第三方来说，那就无法证明这条消息究竟是来自发送者还是接收者。

因此我们需要双方不再共享同一个密钥，而是使用不同的密钥。也就是发送者使用一个自己才知道的私钥生成一个签名，而接收者（或者第三方）则使用另一个不同的密钥对签名进行验证，从而知道这个签名是不是通过发送者的密钥计算出来的，这种看似很神奇的技术其实已经诞生了，就是数字签名技术（digital signature）。

数字签名区分了签名密钥和验证密钥，使用验证密钥是无法生成签名的，此外，签名密钥只能由签名的人持有，而验证密钥则是任何需要验证签名的人都可以持有。

这一部分，和非对称加密的公钥密钥就非常相似了。在公钥密码中，密钥分为加密密钥和解密密钥，用加密密钥无法解密，此外解密密钥只能由需要解密的人持有，而加密密钥是任何需要加密的人都可以持有。

实际上，数字签名就是通过将公钥密码「反过来用」而实现的。

对于公钥密码：

而对于数字签名：

用公钥加密所得到的密文，只能用该公钥配对的私钥才能解密，同样的，用私钥进行加密所得到的密文，也只能用与该私钥配对的公钥才能进行解密，也就是说，如果用某个公钥成功解密了密文，那么就能够证明这段密文，是用与该公钥配对的私钥进行加密的。用私钥进行加密这个行为只能由持有私钥的人完成，基于这一事实，我们才可以将用私钥加密的密文作为签名来对待。

用于公钥是公开的，因此任何人都可以使用公钥进行解密，这就产生了一个很大的好处，即任何人都可以对签名进行验证。

要生成数字签名，通常有两种方法：

直接对消息签名很容易理解：

  1. Alice 使用自己的私钥对消息生成签名（即密文），连同消息一起发送给 Bob
  2. Bob 使用 Alice 的公钥对签名进行解密得到消息再同消息本身进行比对，一致则验证成功

但对整个消息进行加密非常耗时，因此一般都会使用第二种方法，先求出消息本身的散列值，在对散列值进行加密（即签名），无论消息多长，散列值的长度都是固定的。

  1. Alice 使用单向散列函数计算消息的散列值
  2. Alice 使用私钥对散列值进行加密生成签名
  3. Alice 将签名和消息发送给 Bob
  4. Bob 使用 Alice 的公钥对签名进行解密获得散列值
  5. Bob 将签名获得的散列值和 Alice 的消息的散列值进行比对

数字签名是利用了「没有私钥的人无法生成使用该私钥生成的密文」这一性质，它的作用不是用来保证机密性的，可以从上面的流程中看到，发送的消息可以是不经过加密的，它仅仅只代表一种只有持有该私钥的人才能够生成的信息，如果需要保证机密性，则需要再对消息进行加密。

数字签名在很多地方也有具体的应用实例，例如安全信息公告，软件下载，公钥证书，SSL/TLS等等。

数字签名算法，除了前面介绍的 RSA 之外，还有 ElGamal，DSA（Digital Signature Algorithm），Rabin 等算法。

针对公钥密码的中间人攻击也可以应用在数字签名上，要防止中间人攻击，就要确认自己所得到的公钥是不是真的属于自己的通信对象。

实际上要正确使用数字签名，有一个大前提，就是用于验证签名的公钥必须属于真正的发送者，如果公钥被伪造，那么数字签名也就完全失效了。这样似乎陷入了一个困境，数字签名是用来识别篡改，伪装以及否认的，但为此我们必须先得到属于真正的发送者的没有被篡改的公钥！

为了确定公钥是不是合法的，我们需要证书，所谓证书，就是把公钥当作一个消息，由一个可信的第三方来对其进行签名后所得到的公钥。当然，那依然需要对证书上的数字签名进行验证，又需要另一个公钥，要彻底解决这个先有鸡还是先有蛋的死循环问题，就要踏入社会学的领域了，让公钥和数字签名技术成为一种社会性的基础设置，即公钥基础设施（Public Key Infrasturcture），简称 PKI。

证书

证书，也就是公钥证书（Public-Key Certificate， PKC），记载了姓名，组织，邮箱，地址等个人信息，和属于此人的公钥，并由认证机构（Certification Authority， CA）施加数字签名，只要看到证书，我们就可以知道认证机构认定该公钥的确属于此人。

认证机构就是能够认定「公钥确实属于此人」并能生成数字签名的个人或者组织，是一种社会学上的约定。

相比于之前发送者和接收者自行交换公钥，现在我们引入了一个第三方的认证机构，要使用公钥密码进行通信，那么 Bob （发送者）在生成密钥对（也可以让认证机构代为生成）以后，私钥自行保存，公钥则要提交给认证机构，并根据机构的认证业务准则（Certificate Practice Statement，CPS）来进行身份确认。

认证机构使用自己的私钥来对提交的公钥加上数字签名。

当 Alice 需要给 Bob 发送消息时，先从认证机构获得证书，其中包含了 Bob 的公钥和机构的数字签名，Alice 使用认证机构的公钥对数字签名进行验证，验证成功后就获得了合法的 Bob 的公钥。之后 Alice 就可以使用 Bob 的公钥来加密要发送的消息并发送给 Bob。

实际上仅凭证书还不足以支撑公钥的实际运用，还需要制定很多其他的规范，例如证书应该由谁来颁发，如何颁发，私钥泄漏时如何作废证书，计算机之间的数据交换以何种格式等等。公钥基础设施就是为了能更有效的运用公钥而制定的一系列规范和规格的总称。

公钥基础设施（即 PKI）的组成要素主要有以下三个：

认证机构实际上可以用来验证另一个机构的公钥，这样可以形成一个分层迭代的关系，这个关系的最顶点的认证机构，一般就称为根 CA（Root CA），而对于底层如果使用自己的公钥来进行数字签名的行为，则称为自签名（self-signature）

无论是数字签名，证书，还是各种认证机构，都不可能在完全不可信的状态下创造出信任关系。对于认证机构的信任，并不像前面各种加密算法是由数学上严格证明的，而是像信任银行、国家媒体、政府机构一样的社会学上的信任关系，因此这种信任，本质上永远不可能是零风险的。

© 2016-2024 zoubingwu. All rights reserved.